I wrote the below as an entry into 3blue1brown's 'Summer of Math Exposition' competition. It is an introduction to anthropic reasoning, based on the ideas in the book 'Anthropic Bias' by Nick Bostrom. I introduce the main concepts by applying them to the well known Boy/Girl paradox, as a toy example. I've not seen this done elsewhere, and I think it's a nice way to understand the key differences between the competing approaches to anthropic reasoning.
Consider the following claim:
Humans will almost certainly go extinct within 100,000 years or so.
Some may agree with this claim, and some may disagree with it. We could imagine a debate in which a range of issues would need to be considered: How likely are we to solve climate change? Or to avoid nuclear war? How long can the Earth's natural resources last? How likely are we to colonise the stars? But there is one argument which says that we should just accept this claim without worrying about all of those tricky details. It is known as the "Doomsday Argument", and it goes like this:
Suppose instead that humans will flourish for millions of years, with many trillions of individuals eventually being born. If this were true, it would be extremely unlikely for us to find ourselves existing in such an unusual and special position, so early on in human history, with only 60 billion humans born before us. We can therefore reject this possibility as too unlikely to be worth considering, and instead resign ourselves to the fact that doomsday will happen comparatively soon with high probability.
To make this argument a little more persuasively, imagine you had a bucket which you knew contained either 10 balls or 1,000,000 balls, and that the balls were numbered from 1 to 10 or 1 to 1,000,000 respectively. If you drew a ball at random and found that it had a number 7 on it, wouldn't you be willing to bet a lot of money that the bucket contained only 10 balls? The Doomsday argument says we should reason similarly about our own birth rank. That is, the order we appear in human history. Our birth rank is about 60 billion*, so our bucket, the entirety of humanity past, present, and future, is unlikely to be too much bigger than that.
Most people's initial reaction to this argument is that it must be wrong. How could we reach such a dramatic conclusion about the future of humanity with almost no empirical evidence? (You'll notice that we need only know approximately how many people have gone before us). But rejecting this argument turns out to be surprisingly difficult. You might think that there should be an easy answer here. It sounds like a conditional probability problem. Can't we just do the maths? Unfortunately it's not quite that simple. To this day, the validity of the doomsday argument is not a settled question, with intelligent and informed people on both sides of the debate. At heart, it is a problem of philosophy, rather than of mathematics.
In this blogpost, I will try to explain the two main schools of thought in "anthropic reasoning" (the set of ideas for how we should approach problems like this), and why both lead to some extremely counter-intuitive conclusions. We'll start by reviewing a classic paradox in probability theory known as the "Boy or girl paradox", which was first posed as a problem in Scientific American in the 1950s. This paradox will provide a simple concrete example to have in mind when comparing the different approaches to anthropics. The central problem we'll face is how to calculate conditional probabilities when given information that starts with the word "I". Information such as: "I have red hair" or "I am human" or even simply "I exist". How we should update our beliefs based on such "indexical" information is an open problem in philosophy, and given the stakes involved, it seems profoundly important that we try to get it figured out.
*estimates vary
We'll start by reviewing the classic "Boy or Girl paradox", which on the face of it has nothing to do with anthropic reasoning at all. The so-called paradox arises when you consider a question like the following:
Alice has 2 children. One of them is a girl. What is the probability that the other child is also a girl?
It is referred to as a paradox because we can defend two contradictory answers to this question with arguments that appear plausible. Lets see how that works.
Answer A: 1/2. If we assume that each child is born either a boy or a girl with probability 1/2, and that the gender of different children is independent (which we are allowed to assume for the purposes of this problem), then learning the gender of one child should give you no information about the gender of the other.
Answer B: 1/3. The way to justify this answer is with a drawing:
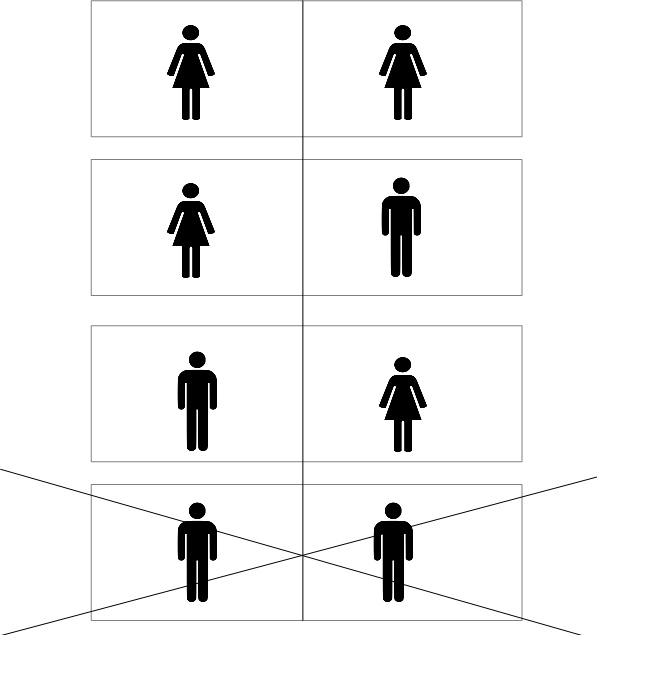
There were initially 4 equally likely possibilities for how Alice's children could have been gendered. When we learn that one of the children is a girl, we can rule out the final possibility shown in the diagram. But we have learnt nothing which allows us to distinguish between the remaining options. Each is still equally likely, and so the probability that both children are girls is now 1/3.
What is going on here? If you've not encountered this problem before you should take a while to think about which answer seems more convincing to you before reading on.
...
So which answer is right? Well actually the question as we phrased it is ambiguous. Both answers could be defended in this context, and that is the source of the apparent paradox. It's helpful to imagine a more precise scenario instead. Suppose we know that Alice has 2 children and we are allowed to ask her a single unambiguous yes/no question. We might ask the following:
Do you have at least 1 girl?
If she answers "yes" to this question, then the probability that both children are girls is actually 1/3. The argument given in Answer B is correct. The argument given in Answer A does not apply, because we have not asked about a specific child in order to learn something about the other (that would indeed be impossible), but have instead asked a question where the answer is sensitive to the gender of both children.
If this still seems unintuitive to you, it might help to remember that before we asked the question, the probability that Alice had two girls was only 1/4. When she answered "yes" it did then increase, from 1/4 to 1/3, it just didn't get all the way to 1/2.
But we might have instead asked the following question:
Is your first child a girl?
If she answers "yes" to this question, then the probability that both children are girls is 1/2. The argument given in Answer A is correct. The argument given in Answer B does not apply, because by asking the question in this way we have also ruled out the penultimate possibility, as well as the first (assuming the children appear in the diagram in their birth order).
There is a third question we could have asked:
Pick one of your children at random, are they a girl?
If she answers "yes" to this question, then the probability that both children are girls is again 1/2. The argument given in Answer A is still correct. It takes a bit more work here to understand how the argument in Answer B needs to change. We need to draw a larger diagram, with 8 possibilities instead of 4. For each possible way the children could be gendered, there are two ways Alice could have selected the children when answering the question. Each of the 8 resulting possibilities are equally likely, and when we carefully figure out which ones have been ruled out by Alice's answer, we can reproduce the 1/2 result:
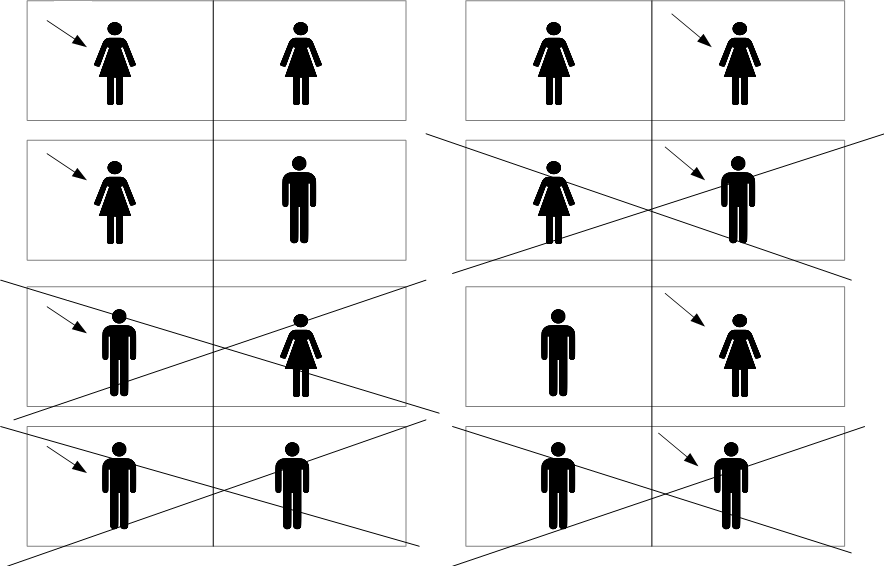
The key take away here is that when you want to update your probabilities based on new information, you sometimes need to think very carefully about how you obtained that information. In the original phrasing of the problem, we were told that one of Alice's children was a girl, but we were not given enough detail about how that fact was discovered, so the answer is ambiguous. If we imagine an unrealistic scenario where we get to ask Alice a single unambiguous question, we can work things through ok. But if we were to encounter a similar problem in the real world then it might not always be clear whether we are in a 1/2 situation or a 1/3 situation, or even somewhere in between the two.
We are now ready to explore anthropic reasoning, and we will do it by continuing to expand the "Boy or Girl paradox" discussed above. We have already seen that the way we obtain the information in this problem is extremely important. And there is one way you could learn about the gender of Alice's children that is particularly tricky to reason about: you could be one of the children.
As before, if we tried to imagine this happening in the real world, all of the information we have from background context would complicate things. To keep things simple, we'll instead suppose that the entire universe contains just two rooms, with one person in each. At the dawn of time, God flipped a fair coin twice, and based on the outcome of the coin toss decided whether to create a boy or a girl in each room. You wake up in this universe in one of the rooms, fully aware of this set-up, and you notice that you are a girl. What is the probability that the other person is also a girl?
Lets try to figure out the answer. First, what information do you gain when you wake up and notice that you are a girl? You might be tempted to say that the only truly objective information you have gained is that "at least one girl exists". If that's right, then the probability that 2 girls exist would be 1/3, as in Answer B. We could draw out the diagram as before:
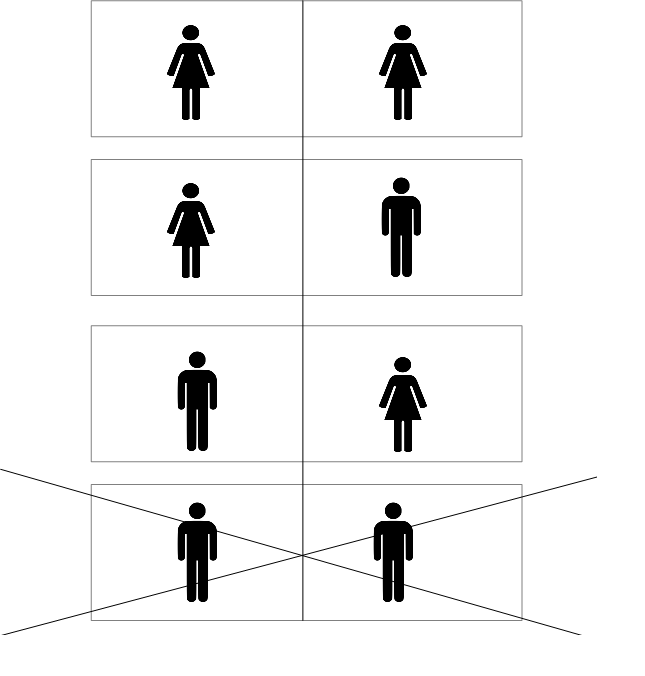
But there's a major problem with this answer (in addition to it being unintuitive). Suppose that the rooms are numbered 1 and 2, with the numbers written on the walls. If you wake up and notice that you are girl in room number 1, the probability that there are 2 girls is now going to be 1/2:
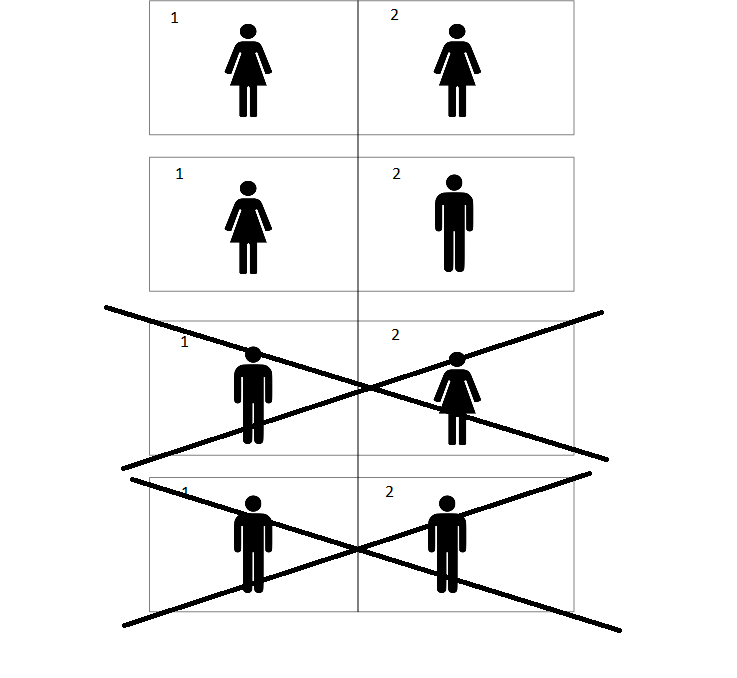
And it's clearly going to be the same if you notice that you are a girl in room number 2.
But what if the number is initially hidden behind a curtain? Before you look behind the curtain, you estimate the probability of 2 girls as 1/3. But you also know that once you look behind the curtain and see your number, your probability will change to 1/2, whatever number you end up seeing! That's absurd! Why do you need to look behind the curtain at all?
The problem here is that we are pretending our information gives us no way of labelling a specific child ("there is at least 1 girl"), when in fact it does "there is at least 1 girl and that girl is you", and that's where the inconsistencies are coming from. To resolve these inconsistencies, we are forced to move beyond the purely objective information we have about the world, and consider so-called "indexical" information as well. In this example it is true that "at least one girl exists". But it is also true that the statement "I am a girl" is true for you, and you need to factor that into your calculations.
How can we go about calculating probabilities with statements like "I am a girl"? The most natural way is to adopt what Nick Bostrom calls the "Self-Sampling Assumption", or SSA. It says that you should reason as if you are a random sample from the set of all observers. This means that when you wake up and find you are a girl, it is the same as in the classic Boy or Girl problem when we asked Alice to randomly select one of her children before answering. We can draw a similar diagram to the one we drew there, with 8 options:
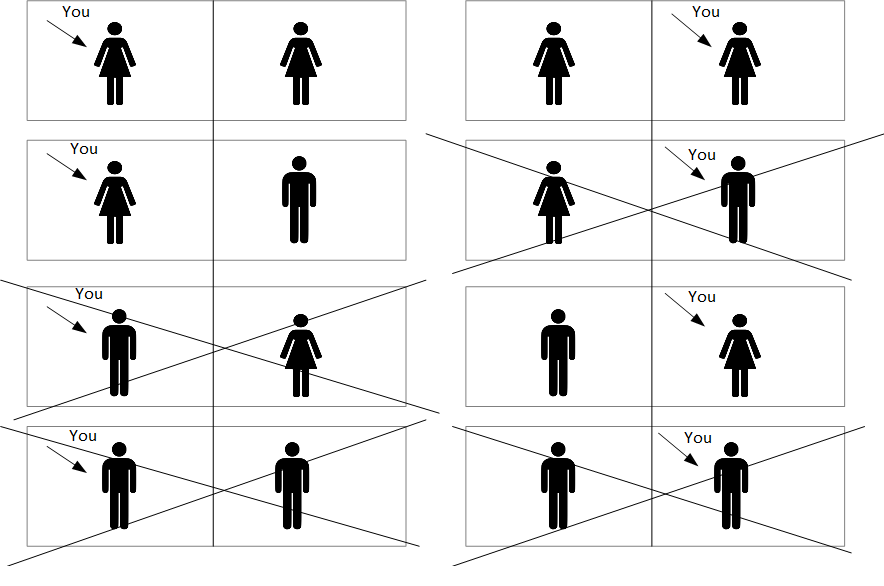
If you accept SSA, The probability that there are 2 girls is then 1/2, whether you look behind the curtain at the number on your wall or not. And the reason that the probability of 2 girls has gone all the way up to 1/2 rather than 1/3 is that it is more likely you would find yourself to be a girl in a world where 2 girls exist than in a world where only 1 girl exists. We are now doing anthropic reasoning!
Ok, so what's the big deal? SSA seems like a natural enough assumption to make, and it gives sensible looking answers in this problem. Haven't we figured out anthropic reasoning? Can we start applying it to more interesting problems yet? Unfortunately things aren't quite that simple.
Imagine we vary the scenario again. Now, when God creates the universe at the dawn of time, instead of creating a girl or a boy based on the outcome of a coin toss, she creates a girl or a rock. SSA tells us that we should reason as if we are a random sample from the set of all observers, but a rock doesn't seem like it should count as an observer. If rocks are not observers, then when you wake up and find yourself to be a girl in this scenario, your estimate of the probability of 2 girls will go back to 1/3 again! It is no longer more likely that you would find yourself a girl in a world with 2 girls compared to a world with 1 girl, because you have to find yourself a girl either way. You could never have been a rock.
This is not as problematic as it might first appear. It could even be that 1/3 is now the right answer. Unlike our previous attempt to justify the answer of 1/3, if we've accepted SSA then it won't now change to 1/2 when we look behind the curtain at our room number. You can see this from the diagram below:
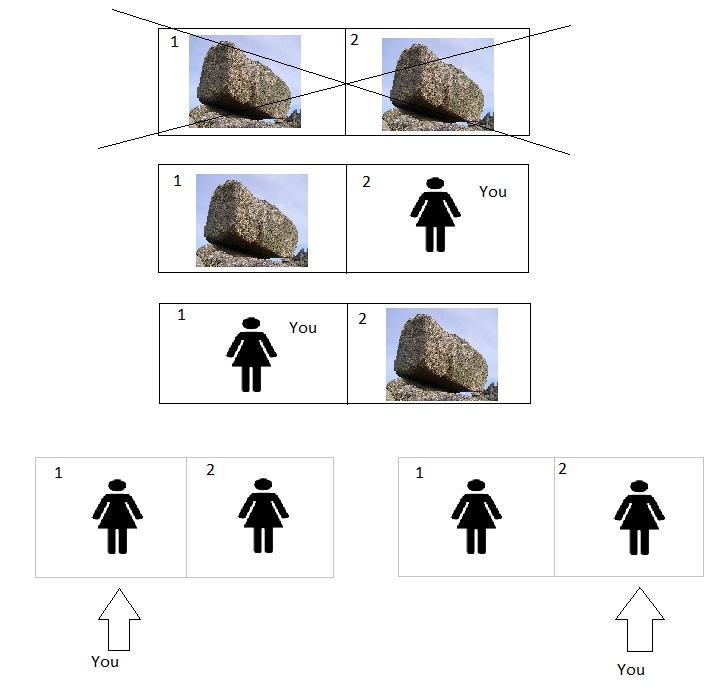
SSA now only comes into play in the bottom row (otherwise you have to find yourself as the girl rather than the rock, since the rock is not an observer). The two bottom row possibilities combine to give an outcome which is equally as likely as each of the three above, so they must each start off with probability 1/8, whereas the other 3 have probability 1/4 (the two possibilities with probability 1/8 have a grey outline to indicate they have half the weight of the others). When you wake up as a girl, you can rule out the top scenario, and the outcomes with a single girl are together twice as likely as the outcomes with two girls (giving a probability of 1/3 of two girls as we said). If you notice a number "1" on the wall after looking behind the curtain, you rule out the second and fifth scenarios, but the remaining single girl outcome is still twice as likely as the remaining two girl outcome, so the probability of two girls is still 1/3.
So unlike our initial attempt at anthropic reasoning where we refused to consider indexical information at all, the 1/3 answer given by SSA here is at least self-consistent. In fact, one school of thought in anthropic reasoning would defend it. But there is still something not entirely satisfying with this. The problem is that our probabilities now depend on our choice of what counts as an observer, our so called "reference class". It might be clear that rocks are not observers, and so the answer was 1/3, but what about jellyfish? Or chimpanzees? Would the answer in those cases be 1/3, or 1/2?
Ok, so suppose we're not happy with this ambiguity, and we want to come up with a way of doing anthropic reasoning that doesn't depend on a choice of reference class of observers. We want an approach which keeps the sensible logic of SSA in the boy/girl case, but also gives the same 1/2 answer in the rock/girl case, or the chimpanzee/girl case. If we consider the diagram above, it's clear that what we need to do is increase the likelihood of the two bottom-row scenarios. We need each of them to have the same probability as the scenarios above. There's one particularly attractive way to do this, which is to add to SSA an additional assumption, called the Self-Indication Assumption, or SIA. It goes like this:
SIA: Given the fact that you exist, you should (other things equal) favour hypotheses according to which many observers exist over hypotheses on which few observers exist.
In other words, given that we exist, we should consider possibilities with more observers in them to be intrinsically more likely than possibilities with fewer observers.
How much more highly should we favour them? To get the answer to come out how we want it to, we need to weight each scenario by the number of observers who exist, so that the two bottom-row scenarios get a double weighting relative to the upper scenarios. If we do this, then taking SSA+SIA together means that our answer to the problem is 1/2, whether we take the boy/girl version, the chimpanzee/girl version, or the rock/girl version.
In general, if we re-weight our different hypotheses in this way, it will completely remove the problem of choosing a reference class of observers from anthropic reasoning. We've seen how that works in the chimpanzee/girl problem, but why does it work in general? Well suppose someone else, Bob, has a definition of "observer" which is larger than ours. Suppose in one of the possible hypotheses, Bob thinks there are twice as many observers as we do. Well SIA will then tell Bob to give a double weighting to that hypothesis, compared to us. But SSA will tell Bob to halve that weighting again. If there are twice as many observers, then it's half as likely that we would find ourselves being the observer who sees what we are seeing. In the end, Bob's probabilities will agree with ours, even though we've defined our reference classes of observers differently.
This is certainly a nice feature of SIA, but how do we justify SIA as an assumption? SSA seemed like a fairly natural assumption to make once we realised that we were forced to include indexical information in our probabilistic model. But SIA seems weirder. Why should your existence make hypotheses with more observers more likely? The lack of good philosophical justification for SIA is the biggest problem with this approach.
We've now seen two different approaches to anthropic reasoning: SSA and SSA+SIA. Both give the answer of 1/2 in the Boy/Girl problem where you wake up and find yourself to be a girl. But they disagree when you change the Boy/Girl problem to a X/Girl problem, where X is something outside of your reference class of observers. In that case, SSA gives the answer of 1/3 while SSA+SIA continues to give the answer of 1/2. SSA+SIA was attractive because our probabilities no longer depend on an arbitrary choice of reference class, but aside from this we are still lacking any good reason to believe in SIA. Before returning to the Doomsday Argument, we'll quickly review an alternative approach to anthropic reasoning called "full non-indexical conditioning", which is effectively equivalent to SSA+SIA in practice, but arguably has a better foundation.
To explain full non-indexical conditioning, we need to go full circle back to when we were trying to think about the Boy/Girl problem without using any indexical information at all (that means no information starting with the word "I"). We thought that the only objective information we had was "at least 1 girl exists", and we saw that reasoning based on that information alone led to absurd conclusions (our probability changes to the same value when we look at our room number, regardless of what number we actually see). But maybe we were too hasty to give up on "non-indexical" conditioning after this setback. Can we think a bit harder to see if there's a way of resolving this problem without invoking SSA at all?
Here's one way to do it. When we said that the only information we had was "at least 1 girl exists", we were ignoring the fact that any observer will necessarily have a whole set of other characteristics in addition to their gender. The information we actually have is not that "at least 1 girl exists", it's that "at least 1 girl with red hair, green eyes, etc and with a particular set of memories exists". If we include all of this information, so the argument goes, we actually end up with a consistent framework for anthropic reasoning which is effectively equivalent to SSA+SIA. If we think of each characteristic as being drawn from some probability distribution, then a particular coincidence of characteristics occurring will be more likely in a world with more observers (SIA), and given a fixed number of observers, the set of characteristics serves as an essentially unique random label for each observer (SSA).
The full details are given in this paper. We mention it here just as an example of how you might try to give a more solid foundation to the SSA+SIA approach.
Now that we're armed with our two approaches to anthropic reasoning (SSA and SSA+SIA), we can return to the Doomsday Argument. The Doomsday Argument said that humanity was likely to go extinct sooner rather than later, because it's very unlikely we'd find ourselves with such a low birth rank in a world where humanity was going to continue existing for millions of years. Is this a valid argument or not?
SSA: Yes, the Doomsday Argument is valid.
Under SSA, our low birth rank is strong evidence that humanity will go extinct sooner. Formalizing this is complicated, because our prior beliefs about the likelihood of human extinction are also important, but for simplicity, suppose that there were only two possibilities for the future of humanity. Also suppose that, leaving aside anthropic arguments, both possibilities seem equally plausible to us:
Doom soon: humanity goes extinct in 10 years
Doom late: humanity goes extinct in 800,000,000 years, with a stable population of around 10 billion throughout that time. If humans have a life expectancy of around 80 years, this means there will be a further (800,000,000 X 10,000,000,000) / 80 = 10^17 humans in the future. This is around a million times more than the number of humans who ever exist in "Doom soon".
If we initially assign a probability of 1/2 to each of these two hypotheses (our "prior"), we can then update these probabilities using SSA and the indexical information of our own birth rank: "I am the 60 billionth human". If we want to visualise this in diagram format as we did above, we would need to draw a lot of images. Here's just a few of them:
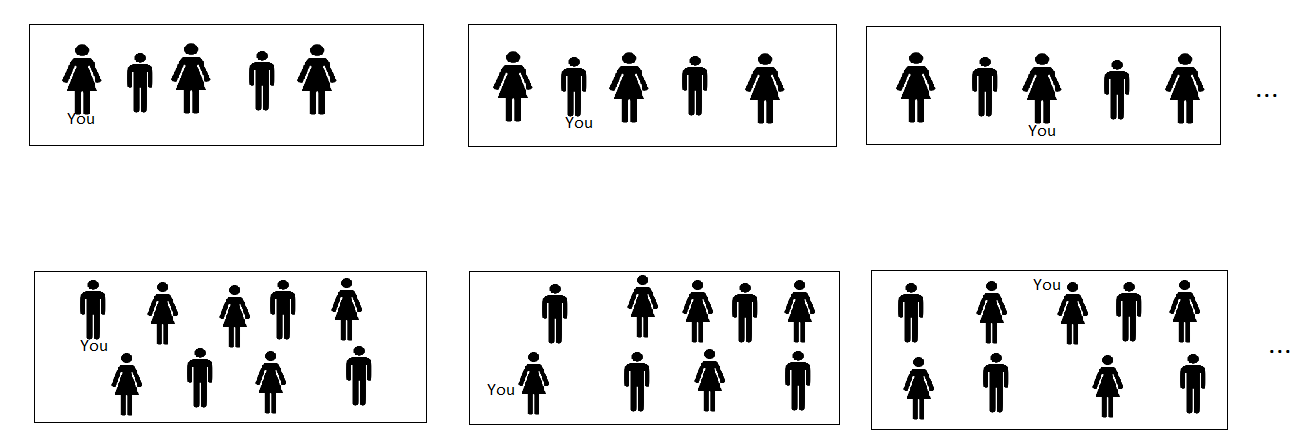
The ones on the top row all combine to give probability 1/2, and there are about 60 billion of them, so they each have probability 1/(2 X 60 billion). The ones on the bottom row all combine to give probability 1/2 as well, but there are 10^17 of them, so they each have probability 1/(2 X 10^17). If you knew your birth rank precisely, you'd eliminate all but 2 diagrams, one from the top row and one from the bottom. The one from the top is around 10^7 times as likely as the one on the bottom, so "Doom soon" is almost certainly true.
This is just the same as drawing a random ball from a bucket which contains either 10 balls or a million balls, finding a number 7, and becoming extremely confident that the bucket contains 10 balls. SSA says we should reason as if we are a random sample from the set of all observers, just like drawing a ball at random from a bucket.
Of course, in practice, "Doom soon" and "Doom late" are not the only two possibilities for the future of humanity, and most people probably wouldn't say that they are equally plausible either. Putting probability estimates on the various possible futures of humanity is going to be extremely complicated. But the point of the Doomsday Argument is that whatever estimates you end up with, once you factor in anthropic reasoning with SSA, those probability estimates need to be updated hugely in favour of hypotheses on which humanity goes extinct sooner.
SSA+SIA: No, the Doomsday Argument is not valid.
If on the other hand we take the approach of SSA+SIA, the Doomsday Argument fails. Our birth rank then tells us nothing at all about the likelihood of human extinction. The reason for this is straightforward. SSA favours hypotheses in which humanity goes extinct sooner, but SIA favours hypotheses in which humanity goes extinct later (because our existence tells us that hypotheses with more observers in them are more likely) and the two effects cancel each other out. If we refer back to the diagram above, after weighting hypotheses by the number of observers they contain, all the drawings are equally likely, and so when we look at the two remaining after using our knowledge about our birth rank, both options are still as likely as each other.
You might now be thinking that the SSA+SIA approach to anthropic reasoning sounds pretty good. It doesn't depend on an arbitrary choice of reference class of observers, and it avoids the counter-intuitive Doomsday Argument. But there's a problem. SSA+SIA leads to a conclusion which is arguably even more ridiculous than the Doomsday Argument. It's called the Presumptuous Philosopher problem, and it goes like this:
It is the year 2100 and physicists have narrowed down the search for a theory of everything to only two remaining plausible candidate theories, T1 and T2 (using considerations from super-duper symmetry). According to T1 the world is very, very big but finite and there are a total of a trillion trillion observers in the cosmos. According to T2, the world is very, very, very big but finite and there are a trillion trillion trillion observers. The super-duper symmetry considerations are indifferent between these two theories. Physicists are preparing a simple experiment that will falsify one of the theories. Enter the presumptuous philosopher: "Hey guys, it is completely unnecessary for you to do the experiment, because I can already show to you that T2 is about a trillion times more likely to be true than T1!
The idea here is that SIA tells us to consider possibilities with more observers in them as intrinsically more likely, but when we take that seriously, as above, it seems to lead to absurd overconfidence about the way the universe is organised.
As Nick Bostrom (who proposed this problem) goes on to say: "one suspects that the Nobel Prize committee would be rather reluctant to award the presumptuous philosopher The Big One for this contribution".
From what we've seen so far, it seems like either we are forced to accept that the Doomsday Argument is correct, or we are forced to accept that the presumptuous philosopher is correct. Both of these options sound counter-intuitive. Is there no approach which lets us disagree with both?
One option is to accept SSA without SIA, but to use the ambiguity in the choice of observer reference class to avoid the more unpalatable consequences of SSA. For example, when considering the Doomsday Argument, if we choose our reference class to exclude observers who exist at different times to us, then the argument fails. We would no longer be a random sample from all the humans who will ever live, but would just be a random sample from all the humans who are alive simultaneously with us, in which case our birth rank is unsurprising. There are problems with saying that observers who live at different times can never be in the same reference class (see Anthropic Bias chapter 4), but maybe we need to adapt our reference class depending on the problem. It could be that reference classes spanning different times are appropriate when solving some problems, but not when evaluating the Doomsday Argument. The problem with this response is that we have no good prescription for choosing the reference class. Choosing the reference class for each problem so as to avoid conclusions we instinctively distrust seems like cheating.
An alternative option is to reject the notion of assigning probabilities to human extinction completely. We did not make this clear in the discussion above, but probabilities can be used in two very different ways:
(A) probabilities can describe frequencies of outcomes in random experiments e.g. the possible ways our children could have been gendered in our imaginary scenario where God flips a fair coin twice.
(B) probabilities can describe degrees of subjective belief in propositions e.g. our degree of belief in the claim that humanity will go extinct within the next 10 years.
(Taken verbatim from Information Theory, Inference, and Learning Algorithms, D.C.J. Mackay)
The use of probabilities in the sense of (A) is uncontroversial, but using them in the sense of (B) is much more so. If we reject their use in this context, then whatever our approach to anthropic reasoning (SSA or SSA+SIA), neither the Doomsday Argument nor the Presumptuous Philosopher conclusion is going to apply to us, because we can't begin to apply anthropic reasoning along these lines unless we have some prior probabilities to begin with.
Rejecting subjective probabilities is one way of escaping the unattractive conclusions we've reached, but it comes with its own problems. To function in the real world and make decisions, we need to have some way of expressing our degrees of belief in different propositions. If we gamble, we do this in an explicit quantitative way. The shortest odds you would accept when betting on a specific outcome might be said to reflect the subjective probability you would assign to that outcome. But even outside of gambling, whenever we make decisions under uncertainty we are implicitly saying something about how likely we think various outcomes are. And there is a theorem known as Cox's theorem which essentially says that if you quantify your degree of certainty in a way which has certain sensible sounding properties, the numbers you come up with will have to obey all of the rules of probability theory.
You might be thinking that all of this sounds interesting, but also very abstract and academic, with no real importance for the real world. I now want to convince you that that's not true at all. I think that asking how long humanity is likely to have left is one of the most important questions there is, and the arguments we've seen have a real bearing on that important question.
Imagine someone offers you the chance to participate in some highly dangerous, but highly enjoyable, activity (think base jumping). If you have your whole life ahead of you, you are likely to reject this offer. But if you had a terminal illness and a few weeks to live, you'd have much less to lose, and so might be more willing to accept.
Similarly, humanity's priorities should depend in a big way on what stage of our history we are at. If humanity is in its old age, with the end coming soon anyway, we shouldn't be too concerned about taking actions which might risk our own extinction. We should focus more on ensuring that the people who are living right now are living good and happy lives. This is the equivalent of saying that a 90 year old shouldn't worry too much about giving up smoking. They should focus instead on enjoying the time they have left.
On the other hand, if humanity is in its adolescence, with a potential long and prosperous future ahead of us, it becomes much more important that we don't risk it all by doing something stupid, like starting a nuclear war, or initiating runaway climate change. In fact, according to a view known as longtermism, this becomes the single most important consideration there is. Reducing the risk of extinction so that future generations can be born might be even more important than improving the lives of people who exist right now.